Afstand houden - oplossing
D.J. Bolt
15-01-22

De puzzel was hoe mensen in een kleine dokterswachtkamer van 2x2m zo ver mogelijk van elkaar kunnen plaatsnemen om de kans op besmetting met virussen te voorkomen.
Als het om drie mensen gaat is het niet zo moeilijk. De beste oplossing is deze:
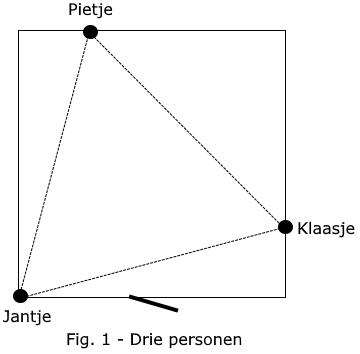
De afstanden tussen de dames kan getekend worden als een driehoek met gelijke zijden.
De lengte daarvan kunnen we berekenen met die beroemde stelling van Pythagoras:
In een rechthoekige driehoek is de som van de kwadraten van de lengtes van de rechthoekszijden gelijk aan het kwadraat van de lengte van de schuine zijde.
Dus c2 = b2 + a2 waarbij c de schuine zijde is en a en b de andere zijden van de driehoek. De grootte van c is dan de wortel uit b2 + a2, geschreven als √(b2 + a2).
We slaan aan het rekenen, zie figuur 2.
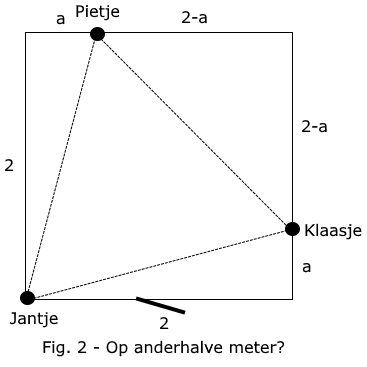
Eerst berekenen we lengte a. Dat doen we door te overwegen dat de afstand tussen Jantje en Pietje gelijk moet zijn aan die van Pietje naar Klaasje. Natuurlijk zijn de kwadraten van de afstanden dan ook aan elkaar gelijk. Dus
22 + a2 = (2-a)2 + (2-a)2 ;
uitgewerkt:
a2 – 8a + 4 = 0
maak er een kwadraat van (een zgn. 'merkwaardig product'):
a2 – 8a + 4 + 12 = 12
dus:
(a – 4)2 = 12
het antwoord is:
a = 4 - √12
opmerking: 4 + √12 is wiskundig ook een oplossing maar ruimtelijk niet.
Nu kan afstand Jantje-Pietje worden berekend, weer met de formule c2 = b2 + a2.
Daarin geldt
c = afstand Jantje-Pietje
b = 2
a = 4 - √12
c2 = 22 + (4 - √12)2
uitgewerkt:
c2 = 32 – 8√12
oftewel:
c = 4√(2-√3)
c = 2,070552 meter.
Ha, zeven centimeter meer dan wanneer ze elk in een hoek waren gaan zitten. Mooi meegenomen dus!
***
Maar nu het lastiger probleem, we moeten met z'n zessen in de wachtkamer. Lukt het om voldoende afstand te houden? En zo niet, hoeveel moet de dokter de ruimte vergroten om aan de 1,5m maatregel te voldoen?

Er is een fraaie oplossing, zie figuur 3.
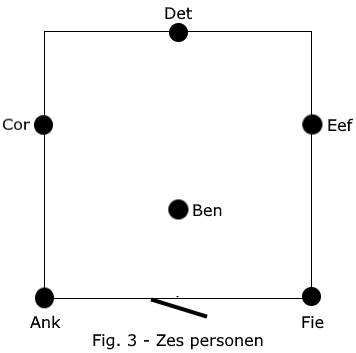
Ank en Ben, Ben en Cor, Cor en Det, Det en Eef, Eef en Ben, Ben en Fie loeren even rond en nemen dan op precies gelijke afstand van elkaar plaats! Maar hoe groot is die afstand? Dat is uit te rekenen als we weten hoever Ben de kamer in mag schuifelen. Dat blijkt 1/3 van de diepte van de kamer te zijn. Kijk maar:
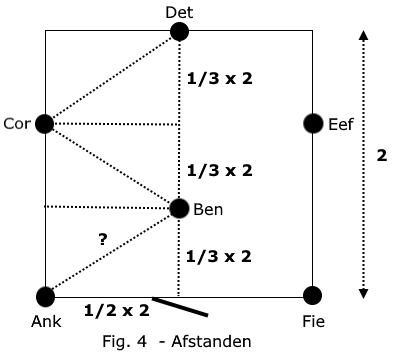
Je kunt namelijk de ruimte in precies 12 gelijke rechthoekige driehoeken verdelen waarvan de diagonalen de gelijke afstanden tussen de mensen aangeven!, zie figuur 4 waar het voor de linkerkant is ingestippeld.
We kunnen die afstand weer berekenen met Pythagoras: c2 = b2 + a2. Dus:
het kwadraat van de afstand tussen Ank en Ben
is gelijk aan.
het kwadraat van de afstand van-Ank-tot-het-midden-van-de-deur
plus
het kwadraat van de afstand van-het- midden-van-de-deur-tot-Ben.
Een hele mond vol maar in formule heel simpel:
Afstand Ank-Ben in het kwadraat = (1/2 x 2)2 + (1/3 x 2)2 , samen 13/9.
Even de wortel er uit trekken, dan blijkt de afstand tussen al deze mensen is 1/3√13, dat is net 1,20m. Daar is onze nieuwe minister van Volksgezondheid Ernst Kuipers dus bepaald niet blij mee …
***
Nou de vraag dan hoeveel de dokter zijn wachtkamer moet uitbreiden zodat deze zes mensen wél op 1,5m afstand van elkaar kunnen plaatsnemen.
We stellen de lengte van de nieuwe wanden op w, zie fig. 5.
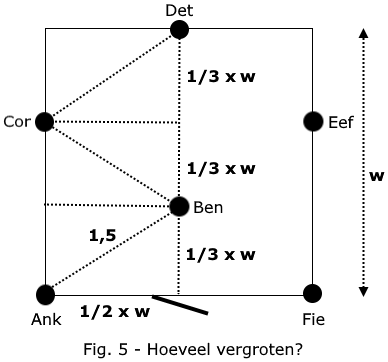
Nu willen we dus dat de afstand Ank-Ben, en dus ook alle andere, 1,5 meter is. We weten dat Ben in het midden zit tussen de linker- en rechterwand, dus op 1/2 w. Ook zit hij in de vergrote kamer weer op 1/3 van de diepte van de kamer, dus op 1/3 w. Hoe groot is die w dan?
We roepen weer Pythagoras te hulp: 1,52 = (1/2 w)2 + (1/3 w)2 samen 13/36w2. Even rommelen, en dan blijkt w gelijk aan 9/√13 te zijn, bijna 2,5. De ruimte moet dus met spoed een half metertje naar alle kanten worden uitgebreid en zie, zelfs zes mensen kunnen veilig op hun vaccinatie wachten!
En nu is onze minister weer dik tevreden!
Wonderlijk!
Onze voortvarende dokter zet zich volop in voor het boosteren. Hij breidt de vaccinatieruimte snel uit met nieuwe wachtkamers zodat hij nog veel meer mensen tegelijk kan ontvangen. Daartoe benut hij het grasveldje rond zijn praktijk op een zeer intelligente wijze. Zo:
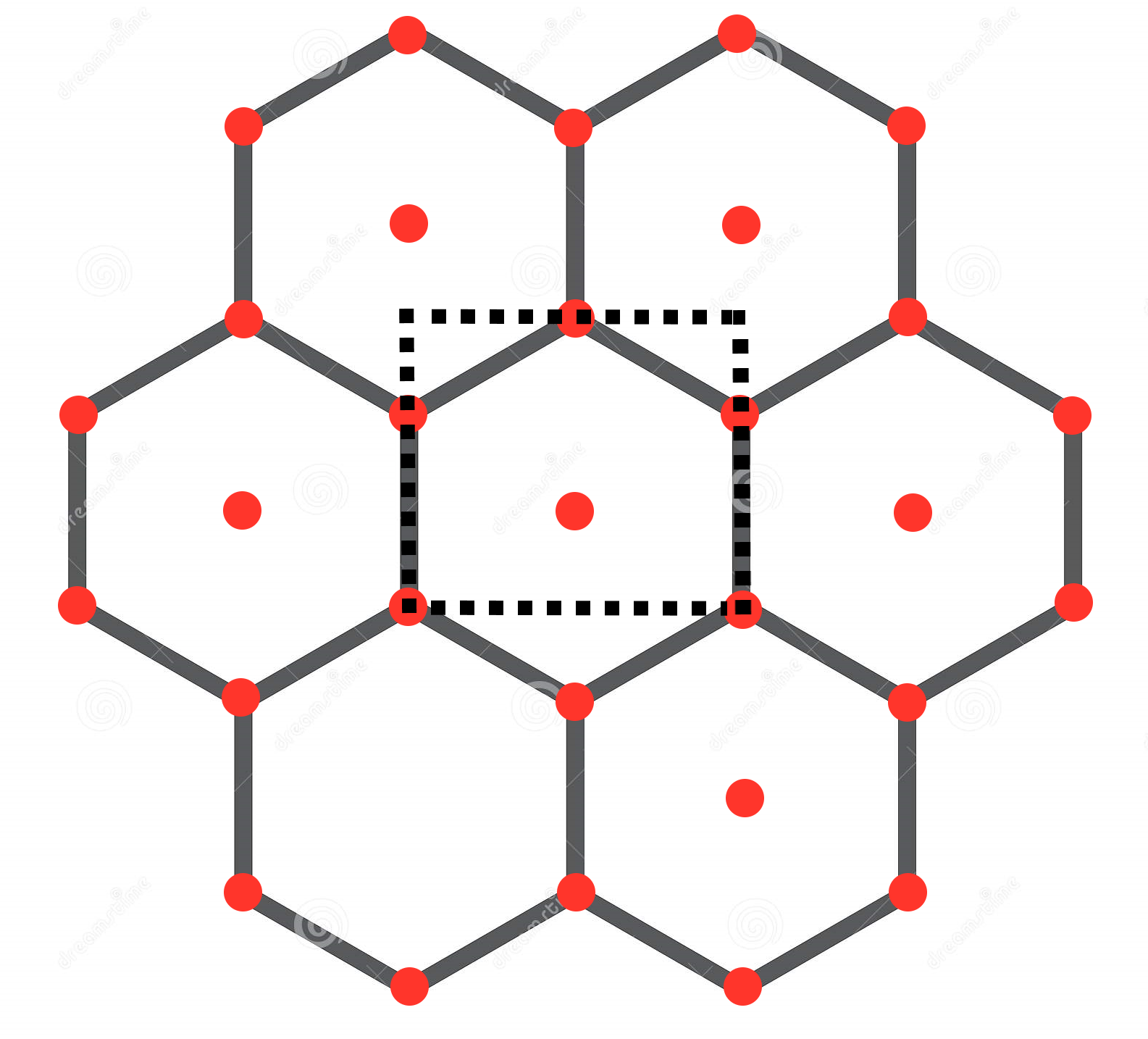
In het midden zien we het oorspronkelijke wachtkamertje (gestippelde lijnen). Daar heeft de dokter een hexacon-vormige, zeskantige ruimte van gemaakt en die heel efficiënt omringd met zes daaraan gelijkvormige kamertjes.
Het totaal aantal personen dat de dokter nu tegelijk ontvangt is, even tellen, dus 7 maal 7 is 49 personen, zie de rode stippen! Alleen de linker-onder wachtruimte mist nog een stoelstipje, maar dat is gereserveerd voor Oebeltje, ze is nog aan het denken of ze zich wel of niet zal laten boosteren.
Misschien hebt u het ook al gezien: het bouwwerk van de dokter is helemaal niet zo origineel. De structuur van zijn nieuwe praktijkruimte heeft hij afgekeken van wat bijen al sinds de schepping bouwen, Want draai de praktijkruimte maar eens een kwartslag
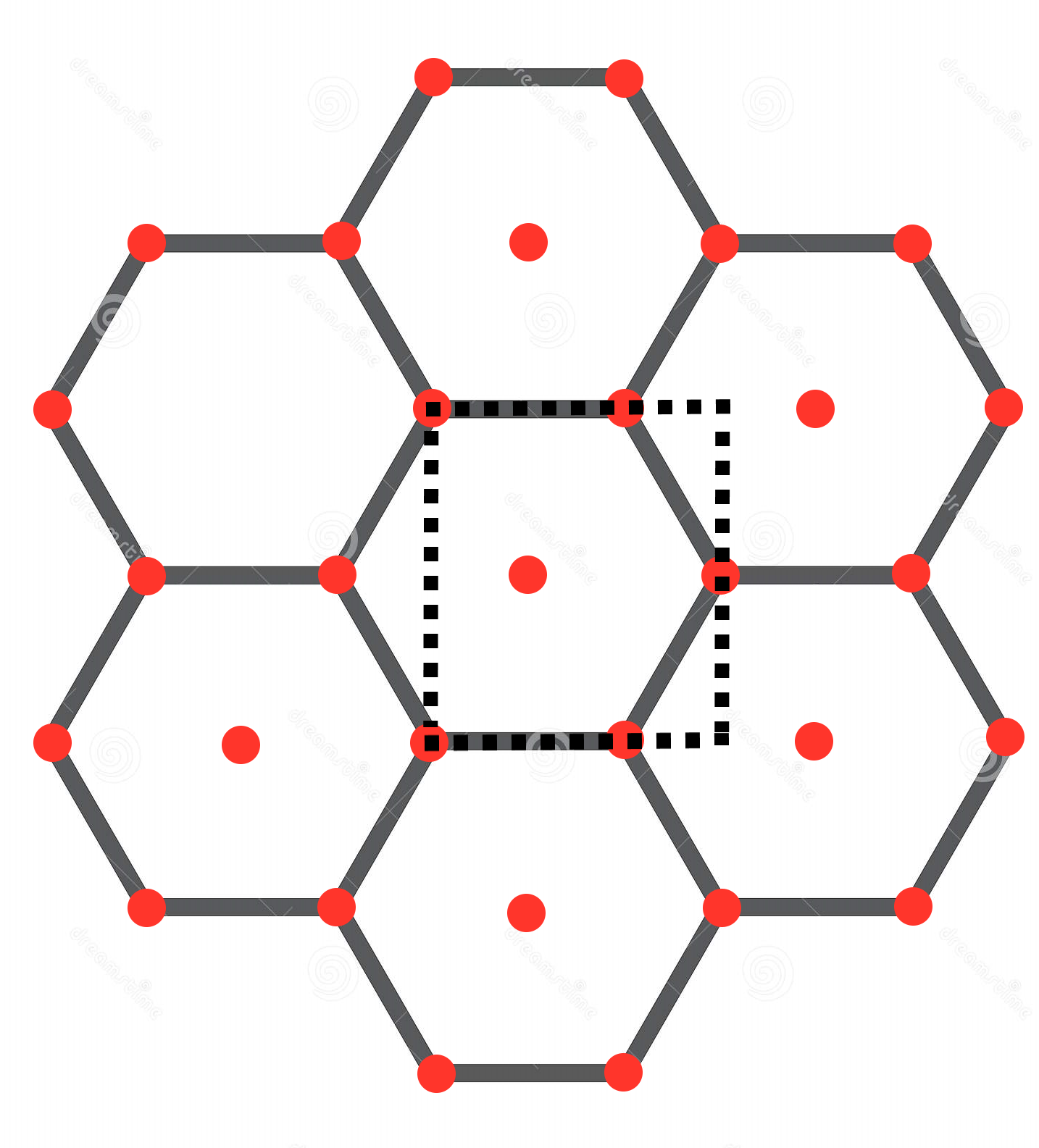
en vergelijk die met de honingraatstructuur.op deze foto:.

Zo'n honingraat bouwen werkbijen van bijenwas. Dat doen ze met hun bovenkaken en poten. De cellen dienen als kraamkamer en als opslagruimte voor stuifmeel en honing. Wanneer ze vol zijn, sluiten de beestjes ze af met een dekseltje. Dat gebeurt ook als een made zich verpopt en dus niet meer gevoerd hoeft te worden.
De zeshoekige vorm van de cellen is de efficiëntste indeling van de raat, die de minste was gebruikt en desondanks stabiel is. Door de zeshoeken hebben de bijen dus de meeste ruimte om honing op te slaan én sparen energie bij de wasproductie. Was is voor de bijen 'duur': de productie van één kilo was 'kost' vier tot zes kilo honing.
Bijzonder, zo komen we via een aardig puzzeltje ineens bij een scheppingswonder. Want de bijen hebben die hexaconische vormen echt niet zelf bedacht. En ook bleek niet na miljoenen jaren van tijd en toeval dat de bijen van deze structuur het minst moe werden en dus hiervoor 'kozen'. Nee, 'gewoon' een indrukwekkend wonder van onze Schepper die Zijn grootheid en intelligentie laat zien in prachtige wiskundige, natuurkundige en biologische structuren.
Lof zij Hem!
