Afstand houden – oplossing 4

D.J. Bolt

26-02-22

De vorige keer gaven we van een lezer de suggestie aan ons adres door, om wat ruimtelijker te gaan denken bij het probleem zes patiënten in een kleine wachtkamer van onze dokter te positioneren. Waarom de wachtkamer verbouwen als de patiënten ook kunnen plaatsnemen op hoge stoeltjes waarbij de corona-afstandsmaatregel van 1,5 meter gewaarborgd is? Dom, dom, dom dat we daar niet aan gedacht hadden. Maar helaas, het was niet bij ons opgekomen!

Maar de spannende vraag is vervolgens natuurlijk wel hoe hoog dan die stoeltjes moeten zijn. Die hebben we berekend en onze lezers daar de vorige keer van mee laten genieten (hopelijk).

Edoch, we hadden even over het hoofd gezien dat de inzender ook al de handschoen had opgenomen en een berekening ingestuurd om zijn eigen probleemstelling op te lossen. Excuus! We laten zijn oplossing hieronder volgen.
En natuurlijk is de spannende vraag of onze oplossingen met elkaar sporen …

Oplossing inzender

De inzender:

'De uitdaging in laatste uitgave van 'Een in waarheid' om de minimale hoogte van de stoelen te berekenen, neem ik aan. Die berekening is niet zo moeilijk.

We leggen een gelijkzijdige driehoek op de vloer van de wachtkamer met op de hoeken de wachtenden A, B en C. Verder construeren we opnieuw een gelijkzijdige driehoek op een hoogte x met de wachtenden D, E en F. Die driehoeken zijn gedraaid ten opzichte van elkaar zodat een bovenaanzicht ontstaat van een zes-puntige ster.

1

Hoe groot kan de zijde zijn van de driehoek zodat de zes-puntige ster in het grondvlak van 2 x 2 meter past?

Daarvoor hebben we de tangens van 15 ⁰ nodig (= 0,26795) en wat gereken met A² + B² = C² (kent u Pythagoras nog?). De uitkomst is dat die zijde 207,06 cm is. A, B en C evenals D, E en F zitten 207,06 cm bij elkaar vandaan.

2

Hoe hoog moet de 2^e driehoek boven de onderste komen liggen zodat de afstand tussen de wachtenden A, B en C 1,50 meter is naar de wachten D, E en F. Ook dat is te berekenen met enig ge-Pythagoras en daar komt uit, dat die hoogte 108,55 cm moet zijn. Stoelen met een zitvlakhoogte van 109 cm lijken te voldoen. Het gevoel van D.J. Bolt, dat een hoogte van 130 cm wel wat minder kan zijn, lijkt juist te zijn.'

Tot zover in eerste instantie de aritmetische oplossing van de inzender. En zoals de Spreukendichter al zei: 'de eerste spreker heeft altijd gelijk maar dan komt de volgende, die rekent hem na'.

Gaan we doen.

Nagerekend

We zijn het helemaal eens met de deeloplossing die onder 1 is aangegeven. Dit antwoord hebben wij ook gevonden, click hier.

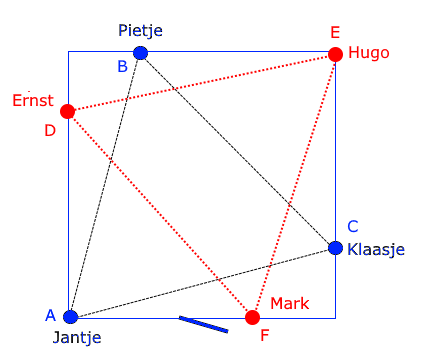
Vanaf de zolder gezien zitten de zes personen er dus zo bij volgens de

'zespuntige ster':

Maar bij deeloplossing 2 krabben we ons toch wat achter de oren. De inzender berekent de minimale stoelhoogte op 108,55 cm. Maar wij vonden 104,9405 cm!, click hier.

We willen niet kinderachtig doen en kijken dus niet op een paar centimeter. Maar net als de boekhouder die bij een dubbeltje verschil op de balans net zo lang zoekt tot hij de fout gevonden heeft – het verschil kan toch ergens een grove fout signaleren?! – doen wij dat ook.

De vraag is dus: vanwaar dit verschil?

We denken het gevonden te hebben en proberen dat te illustreren met het volgende plaatje.

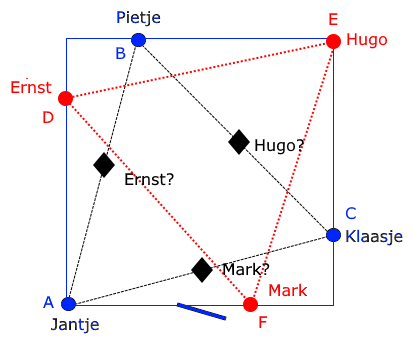
De inzender heeft de stoeltjes niet op de rooie punten gezet maar op de posities met zwarte wybertjes aangeduid. Dus halverwege Jantje-Pietje, Pietje-Klaasje, Klaasje-Jantje. Denken we.
Laten we maar eens wat focussen op die situatie.

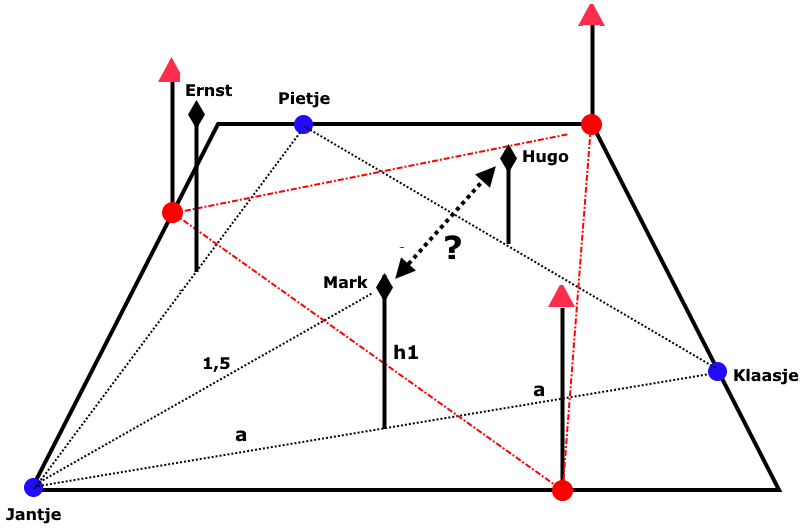
De stoelhoogte h1 valt gemakkelijk te berekenen. Hierboven had inzender de afstand Jantje-Klaasje al berekend op 2,0706. Mark zit op de helft daarvan volgens de inzender (denken we). En dus met Pythagoras is

h1² = √(1,5²  - (1,0358)² )

h1= 1,084951, afgerond 1,0855.

En dat is precies wat inzender berekende! Dus zal hij de stoeltjes zo neerzetten (denken nog meer).

Ruimtelijk denken

De inzender maande ons de vorige editie ruimtelijker te denken. Dat doet hij nu weer:

'In mijn vorige bijdrage had ik aangegeven dat we moeten leren wat ruimer en ruimtelijker te gaan denken. Is het wel verantwoord om vier [hij zal 3 bedoelen, djb] van de zes wachtenden met hun mond en neus tegen de muur te drukken (zodat ze niet meer kunnen ademen en covid-19 verspreiden).'

Ja, dat is toch onmenselijk, hoe hebben we het kunnen bedenken! Dáárom heeft inzender natuurlijk de stoeltjes verder in de ruimte gezet en niet tegen de muur.
Maar we hebben het ruimtelijke advies ter harte genomen en daarin geoefend de afgelopen veertien dagen. Dus leefden we ons verder in in de ruimte van inzenders oplossing.

We kwamen tot een onthutsende conclusie! Want heeft inzender zelf wel voldoende de ruimtelijke situatie van Mark t.o.v. Hugo ingedacht, en ook die van Mark t.o.v. Ernst? Zitten zij nog wel 1,5 meter van elkaar, daar hoog in de lucht?
We gaan weer even rekenen.

't Is heel eenvoudig. De driehoek Jantje-Pietje-Klaasje heeft gelijke zijden, een zgn. gelijkzijdig driehoek. Daarin zijn de drie vrienden als volgt gepositioneerd:.

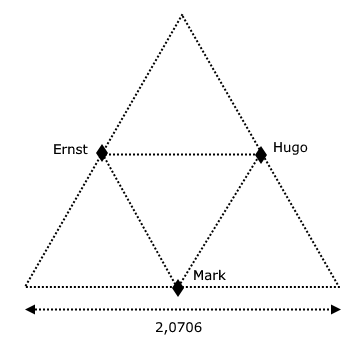
Ieder ziet onmiddellijk dat de afstand tussen hen de helft van 2.0706 moet zijn, dus 1,0358! Ergo, foei inzender, dat is geen anderhalve meter!

Vermaan

Het vermaan van de inzender aan ons wordt trouwens nog indringender en krijgt zelfs een religieuze trek:

'Of nog erger: mogen we als schepselen van God onze wachtende medemensen reduceren tot een meetkundig punt? Dan is de 'menselijke maat' zoek en is er in zekere zin sprake van 'grensoverschrijdend gedrag'. Laten we elkaar wat leefruimte gunnen en niet met het gezicht naar de muur gaan zitten. Laten er rekening mee houden dat niet bij iedereen de afstand van mond en neus tot het zitvlak gelijk is en verschillend is. Onze ademhoogte en misschien ook wel 'toonhoogte' verschilt. Dat maakt dat stoelen met een zithoogte van 109 cm niet voldoen. Ik ben om die reden uitgekomen bij een redelijke schatting van 130 cm of ben ik nu te ruim denkend? Of komt de 'waarheid' nu toch nog in het midden te liggen?'

Waardevolle opmerkingen! We gaan samen met de inzender naar een praktische (grotere) stoelhoogte zoeken. Want inderdaad zitten onze neuzen niet allemaal op dezelfde hoogte. Én, kennelijk wijst inzenders neus en die van mij ook niet dezelfde kant op. Want waarom wijst zijn neus naar de muur en die van mij de wijde ruimte in? Dus zo >

Zo kunnen Mark, Hugo en Ernst ook nog eens het hele 'heer' overzien. Dat is echt ruimtelijk toch?! Als ik het ook wat geestelijk mag duiden: '… bij mij vind u niet te weinig ruimte maar in uw binnenste is het te eng… 2Cor. 6:12

En honoreren we nog graag inzenders vraag

'Wat leert de Bijbel ons over de maat waarmee we meten? (Mat. 7 : 1 e.v.)

Het bekende antwoord is: Met die maat worden we zelf gemeten!
Precies, en daarom namen we inzenders afmetingen de maat, en ontdekten dat die toch niet aan Rom. 13 voldoen.

Rest mij om inzender gemeend hartelijk te danken voor zijn bijdrage die mij aangename uurtjes heeft bezorgd!