Onmogelijk
D.J. Bolt
03-04-21
Eva en Evert zijn dol op legpuzzelen. Als het even kan proberen ze elke avond er eentje te leggen om te ontdekken wat de plaat voorstelt. Ontdekken, ja want ze doen het een beetje anders dan 'gewone' puzzelaars. De puzzelstukjes worden aan het begin van het spel op de kop gelegd! Daarna mag ieder om de beurt een willekeurig stukje pakken en dat proberen te leggen. Ze hebben er een wedstrijdje van gemaakt: het gaat erom wie de meeste stukjes op een avond heeft gelegd. Daarbij is de afspraak dat iemand mag doorgaan met leggen zolang hij of zij dat kan, daarna is het de beurt van de ander.
---
Op een gedenkwaardig avond deze winter zetten Eva en Evert zich weer om hun spelletje te spelen. Volgens de leverancier zou de oplossing van de puzzel 'een prachtige natuurfoto' opleveren. Vol verwachting begint het echtpaar aan de 1000-stukjes legplaat.
Eva mocht starten want zij had de vorige keer verloren. Ze nam het eerste stukje en legde het midden op de tafel. Het volgende stukje bleek ook te passen. En, het derde ook! Oh wonder, het hield niet op, ze legde maar door, en door, en door…
Everts gezicht betrok. Dit was toch niet normáál? Maar toen ze het 500ste stukje had gelegd riep hij ineens: ik zie het, het wordt een dinosaurus. Nu zag Eva het ook. Prachtig, dat enorme beest waarvan nu nog maar slechts stukjes van het achterlijf met poten was gelegd.
Dinosaurussen zijn 66 miljoen jaar geleden uitgestorven, zei Evert op een toontje dat hij als leraar biologie altijd aansloeg als hij hiaten in kennis bij zijn vrouw wilde dempen. De eerste levende cel, ongeveer 4 miljard jaar geleden werd gevormd uit atomen en moleculen, evolueerde uiteindelijk tot dit enorme beest, gewéldig niet?
Eva keek hem glimlachend aan. Zullen we verder gaan?, zei ze. Evert gromde, had er eigenlijk niet zoveel zin meer in, het was toch al een hopeloos verloren spel immers. Maar Eva pakte weer een stukje uit de doos, en legde het na enige aarzeling precies op de goede plaats. Het was nu ook minder zoeken naar de juist plek nu duidelijk was wat de plaat voorstelde.
En niet te geloven, ze bleef pakken, leggen, pakken, leggen, pakken….
Laatste!, opgelost!, jubelde ze, gewonnen!
Kan niet, steunde Evert, o n m o g e l i j k !
Je was erbij, je ziet het toch, spotte Eva, wrijf je ogen eens uit. Er is gewoon een kans dat dít een keer gebeurt, en het ís nu gebeurd! Kijk niet zo sip en ga koffiezetten dan zal ik even uitrekenen hoe groot de kans was die vanavond werkelijkheid is geworden.
---
Evert slofte weg en Eva die wiskunde in haar pakket had gehad, sloeg aan het rekenen. Het duurde wel even want het was toch minder eenvoudig dan ze eerst had gedacht. Maar het lukte!
Even later kwam Evert met twee dampende koppen koffie aan. Ik heb er ook maar even twee gebakjes uit de koelkast bij gedaan, zei hij, voor mij tot troost en beloning voor jou. Nou, hoe groot is die kans?
Wel, zei Eva, de kans is niet 1 op de miljoen, niet 1 op de triljoen, dat is een 1 met 18 nullen, maar minder dan 1 op …, nou ik zal het even voor je opschrijven:
de kans is minder dan 1 op 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000, oftewel een 1 met 172 nullen! Dezelfde kans als 172 keer achter elkaar een 3 te gooien met een dobbelsteen die in plaats van 6, 10 kanten heeft!
Onmogelijk dus, herhaalde Evert zijn eerdere conclusie, de kans dat jij toevallig alle 1000 stukjes gelijk kan wegleggen is núl. Of je moet een zowat eeuwig leven om het een keer mee te maken.
---
Peinzend keek Eva haar man aan. Ik ben het met je eens, zei ze rustig, die kans is zó oneindig klein dat dit wonder vanavond hier ook niet is gebeurd.
Huh, wat zeg je me nou, verwonderde Evert zich, we zagen het toch gebeuren zei je. Hij keek Eva met grote ogen aan.
Nee, zei Eva, ik heb je bedot. Als je even goed kijkt, zie je dat ik, vrijwel onzichtbaar als je het niet weet, de coördinaten op de onderkant van de stukjes hebben aangegeven.
Nu zag Evert het ook. Boef, riep hij, je hebt me bedrogen!
Dat is zo, beaamde zijn vrouw, maar daarmee wilde ik jóu es een lesje leren. Want je blijft maar volhouden, en je deed het tijdens dit spelletje wéér, dat de eerste levende cel door tijd en toeval zou zijn ontstaan. Die meest eenvoudige cel die zovéél ingewikkelder in elkaar steekt dan dit stomme puzzeltje van 1000 stukjes. Laat me een stukje voorlezen uit een artikel dat onder de provocerende titel 'En de mens schiep leven' staat op de site van jouw universiteit[1]. Daar schrijft de Groningse dr. H.F. Boersma over het maken van synthetisch leven, het samenstellen van een levende cel. Het schijnt razend ingewikkeld te zijn:
'Om het niet te moeilijk te maken, begon Venter [Amerikaanse wetenschapper, djb] met het kleinst bekende genoom [alle genen samen, djb] waarvan wetenschappers het bestaan kennen, dat van Mycoplasma genitalium. Deze parasiet, die leeft in het voortplantings- en ademhalingssysteem van primaten, bezit maar 470 genen en heeft een grootte van ongeveer 580.000 basenparen. Hij kan met een relatief klein genoom toe, omdat hij uitgebreid teert op door zijn gastheer geproduceerde voedingsstoffen.
Het lijkt zo gemakkelijk, DNA synthetiseren; een druk op de knop en het gewenste DNA rolt uit de synthesizer. Toch zijn de apparaten die wetenschappers tot nu toe gebruiken om de onderdelen van het DNA aaneen te rijgen nog notoir onbetrouwbaar en langzaam.
De chemische reacties die ten grondslag liggen aan het aan elkaar zetten van de basen, zijn omslachtig en moeilijk te controleren. De reactie mislukt regelmatig, met als gevolg dat er een verkeerde DNA - volgorde uit het apparaat rolt. Dat betekent dat men elk gemaakt stuk moet controleren en soms herstellen. Het is daarom alleen efficiënt om kleine stukken te maken, daar de goed gelukte uit te kiezen en die vervolgens aan elkaar te lijmen – monnikenwerk.'
Wil je beweren dat het niet kan lukken?, vroeg Evert uitdagend.
Nee, dat beweer ik niet, antwoordde Eva. Maar dit artikel werd 10 jaar geleden geschreven, en nog steeds is het de knapste koppen van wetenschap niet gelukt om een volledig zelfstandig werkende levende cel die zichzelf dus kan reproduceren, in het lab te fabriceren uit dood materiaal. Het zal met ongelooflijk veel menselijke creativiteit en groot wetenschappelijk vernuft misschien een keer gaan lukken. Maar mijn punt is dat jij denkt dat die cel ooit zomaar vanzelf, door 'Tijd & Toeval', tot leven kwam.
Het was volgens jou onmogelijk dat onze legpuzzel zó tot stand kwam. En je hebt gelijk. Maar een van de kleinste cellen die oneindig ingewikkelder is dan die stomme puzzel, een cel immers bestaande uit niet minder 470 genen met ongeveer 580.000 basenparen - die tegelijk moeten werken en in precies de goede volgorde moeten liggen - zou vanzelf es een keer moeten zijn ontstaan en tot leven gekomen?
Voor de kans daarop heb ik geen nullen genoeg. Op mijn beurt zeg ik nu:
o n m o g e l i j k !
Begrijp je?
Bereken de kans
Voor degenen die net als Eva graag rekenen, hierbij de manier waarop de oplossing is gebaseerd.
De vraag is dus hoe groot de kans is dat 1000 legpuzzelstukjes, willekeurig gepakt, achterelkaar weggelegd kunnen worden.
De kans dat een gepakt stukje past hangt natuurlijk af van de hoeveelheid vrije aanlegplekjes, 'slotjes' die er op dat moment beschikbaar zijn in het al gelegde gedeelte van de puzzel. Bij het allereerste stukje zijn dat vier, immers aan vier kanten kan er een nieuw stukje worden aangelegd. Maar bij elk volgend stukje kan het totaal aantal aanlegplekjes veranderen. Met hoeveel, laat het plaatje laat zien, er zijn vier mogelijkheden:
Stukje 1: Van z'n vier 'slotjes' wordt 1 gebruikt om aan te leggen, dus zijn er drie vrije slotjes over. Maar het totaal aantal vrije slotjes is niet met 3 maar slechts met 2 toegenomen want het stukje bezet zelf één van de al bestaande aanlegplekjes, dus de toename van het totaal aan 'vrije slotjes' is 3 – 1 = 2.
En zo blijkt stukje 2 het totaal met 1 te vermeerderen, en in de situatie van stukje 3 blijft het totaal aantal vrije slotjes gelijk, terwijl als stukje 4 gelegd wordt het totaal zelfs met 1 afneemt!
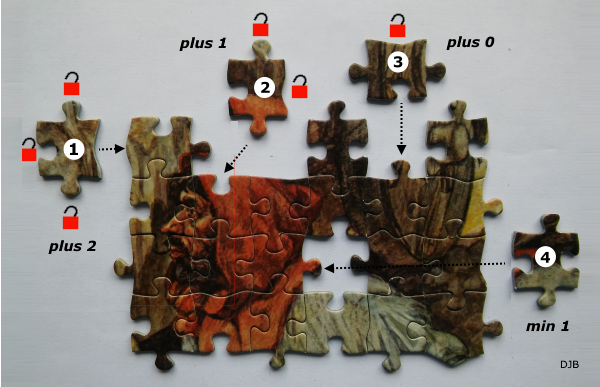
Het is vrijwel onmogelijk om uit de haast ontelbare mogelijke volgorden waarin stukjes kunnen worden gelegd de gevraagde kans te berekenen. Maar wat we wél kunnen doen is, uitrekenen wat de grootst mogelijke kans is dat elk gepakt stukje past en zo het plaatje in één 'run' klaar is. Die grootst mogelijke kans is als het totaal aantal vrije slotjes per gelegd stukje steeds met 2 zou toenemen (dus net als bij stukje 1 in het plaatje):
Eerste stukje gelegd : totaal 4 vrije slotjes
Tweede stukje gelegd : totaal 6 vrije slotjes
Derde stukje gelegd : totaal 8 vrije slotjes
Enzovoort.
De kans dat Eva een passend stukje pakt blijft zo dus maar groeien. Tot hoever?
Het is grappig, maar er komt een moment dat de kans daarop 100% is. Namelijk als het totaal aantal vrije slotjes net zo groot is als het aantal stukjes dat nog in de doos ligt! Een eenvoudig sommetje leert dat dit het geval is als Eva 333 stukjes heeft gelegd. Immers dan zijn er 2 x 333 = 666 vrije slotjes en liggen er nog 666 stukjes in de doos (het eerste stukje vergeten we maar even). Elk stukje kan daarna met zekerheid worden aangelegd[2].
We zullen met een voorbeeld de berekening van de gevraagde kans toelichten.
Eva pakt het 250ste stukje, in de doos liggen dan nog 1000 - 250 = 750 stukjes - en er zijn dan 500 vrije slotjes. De kans dat dit stukje past is dus aantal vrije slotjes gedeeld door aantal stukjes nog in doos, oftewel 500 gedeeld door 750, de kans is dus tweederde. Zo kan voor ieder individueel stukje (onder de 333) de kans dat het past worden berekend.
De totale kans is dan: de kans dat stukje 1 past maal de kans dat stukje 2 past… maal de kans dat stukje 332 past maal 1 voor alle volgende stukjes.
Het antwoord kan zonder wiskunde gemakkelijk worden berekend met een Excel spreadsheet. De uitkomst is:
De kans dat Eva alle stukjes in één keer legt is kleiner dan die 1 op 1.000…000…000: een 1 met 175 nullen!
Dus onvoorstelbaar klein.
Als wiskundige formule geschreven:
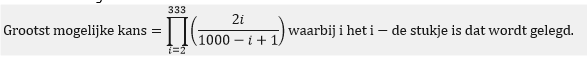
Zo kan Excel de totale kans berekenen
Voor wie het leuk vindt zelf het antwoord te zien verschijnen, kan een spreadsheet zó worden ingericht:
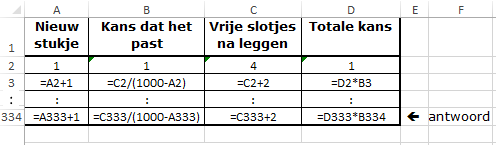
- Zet de aangegeven waarden in de rijen 1 en 2.
- Plaats de aangegeven formules in rij 3 als formules in deze rij.
- Kopieer de formules in rij 3 naar de rijen 4 tot en met 334.
- Het antwoord verschijnt in D334.
Veel plezier!
NOTEN
[1] Voor het hele artikel, click hier.
[2] Het totaal aantal vrije slotjes kan nog weer minder worden dan het aantal te leggen stukjes. Dat is het geval als er stukjes worden gelegd als stukje 4 in het plaatje. Maar daar rekenen we niet mee omdat het ons gaat om de de grootst mogelijke kans te berekenen.
